今天瀏覽百度知道 發現一個問題,有一個網友在問:Φ48*35mm鋼管橫向承載力怎么算?如下圖:
另外本站(常州精密鋼管博客m.youwin2019.com) 也有網友在問:
一根48×3.5國標鋼管所能承受的力為多大
工地上使用的直徑48mm,壁厚3.5mm的鋼管立桿,一根能承受多大的力?
針對上以問題,我們作了下面的回答:
優質解答
當鋼管步距為1500mm,此時計算長度L0=1500mm,回轉半徑i==15.78mm,則有:
長細比λ=L/i=,1500/15.78=95
經查閱資料得穩定系數φ=0.512,
容許荷載[N]=φAf=0.512×489×205=51325N=5.13噸詳細的分析如下:Ф48×3.5鋼管支承桿的承載能力
一、現行規范的不適應
要在滑模工程中推行大噸位液壓滑模千斤頂首先必須解決鋼管支承桿的承載能力計算問題。支承桿從Ф25鋼筋換成Ф48×3.5鋼管,由于J值從1.91cm4增至12.19cm4,剛度增加了5倍多。那么其承載能力是否也以此倍數增加呢?按《液壓滑動模板施工技術規范》(GBJ113-87)附錄三規定,支承桿承載能力的計算公式為: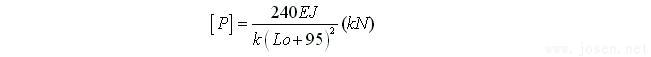
該公式是按當時常用的Ф25,Ф28實心支承桿通過試驗歸納出來的經驗表達式,當前推行大噸位千斤頂以Ф48×3.5鋼管作支承桿時,再采用(GBJ113-87)中的公式計算承載力顯然會得出不正確的結果。以最常見的構造尺寸為例:每次提升30cm,模板上口到提升架下模梁下口高度50cm,下模梁下口到千斤頂下卡頭距離25cm。以上數據代入上式
Lo=30+50+25+=105cm E=2.1×104kN/cm2
J=12.19cm4 有套管λ=1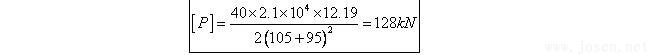
事實上因為Ф48×3.5鋼管的截面積僅4.89cm2。3號鋼的屈服點強度標注值是240N/mm2。當鋼管到達屈服點時的承載能力應是
4.89×100×240=117360N=117.36kN<128kN
鋼管內應力如超過屈服點,變形就急劇增加,支承桿就出現失穩現象,所以不允許應力達到屈服點,其承載能力不允許達到117kN,當然更不可能用到128kN。由此可以肯定(GBJ113-87)附錄三的支承桿承載能力計算公式不使用于Ф48或更大的鋼管。
二、尋求使用的方法
有人建議按照《鋼結構設計規范》(GBJ-17-88)進行計算。按照規范中5.1.2公式 計算,取f=200N/mm2。可是這本規范用的是以概念理論為基礎的極限狀態設計方法。它不是用一個總的安全系數,而是采用了多個分項系數的極限狀態計算方法。雖然3號鋼的抗力分項系數很明確,規范中已有了明確的強度設計值(200或215N/mm2),但是荷載的分項系數卻不明確。特別是我們的活荷載情況復雜,難以確定。這種計算方法與《滑模施工技術規范》截然不同,難以統一,因此目前尚不可能直接按《鋼結構設計規范》(GBJ17-88)的公式進行計算。
從形式上看GBJ113-87附錄三的支承桿能力計算公式,似以歐拉公式為基礎,即近似的看作支承桿上下兩端為固結(即μ=0.5),上端為千斤頂的下卡頭,下端在混凝土表面以下95cm處(若模板長120cm則基本上是模板下口附近)。以上述數據代入歐拉公式則有:
這個數值基本上相當于φ25鋼筋作支承桿的承載能力3倍左右。
七、上述方法的可行性
現以φ25鋼筋作支承桿求其承載能力,以兩種計算方法作對比進行計算。
對比兩者計算結果,對于有套管的工具式支承桿N=fφA公式計算結果是偏于安全的。而對于非工具式支承桿則是偏大20%左右。由此是否可肯定這個方法基本是可用的。特別是用φ48×3.5鋼管做支承桿的大多數是工具式支撐桿,工程進行中或是完成后要拔出來的。對于個別的不準備拔出的也無妨增設一個套管,這樣也可減少提升架的類型。再說為了減少一根套管而要增加20%-30%的千斤頂是不值得的。
八、幾個問題的探討
1、φ48×3.5鋼管與φ25鋼筋支承桿承載力的比較。在我們剛開始研究以φ48×3.5鋼管作支承桿時曾認為由于其剛度是φ25鋼筋的6倍,所以其承載能力也是6倍。如果上述的計算方法成立的話,這個觀點根本概念是錯的。應該說在一般正常滑升的情況下φ48×3.5鋼管與φ25鋼筋作支承桿其承載能力之比是3左右。這個比值隨支承桿脫空長度的增長而增長。當脫空長度(混凝土面至千斤頂下卡頭的距離)從90cm增至205cm則此比值從2.6增至4.8。由此可見越是脫空長度大的情況下用鋼管做支承桿越有利。如支承桿經過門窗洞口時就是如此。我們在一次應用鋼管支承桿過一門洞時未做加固安然通過。雖然是荷載較小,但若是用φ25鋼筋作支承桿再大的荷載也不可能不加固。
2、以上計算均采用k=2的安全系數,但是實際上φ48×3.5鋼管支承桿的安全度比φ25鋼筋的高。有過滑模施工經驗的人都知道,在高層建筑滑模時,用φ25鋼筋作支承桿在十層以下很少有支承桿失穩的。可是越往上滑升支承桿失穩現象就逐漸增加。究其原因無非是平臺不平、模板變形、高處風荷載大等給支承桿帶來側向荷載、附加荷載、偏心荷載。由于φ25鋼筋剛度小抵抗偏心荷載能力小,而φ48×3.5鋼管剛度是它的6倍,其抵抗這些不正常荷載的能力大大提高,絕不是計算的承載能力增長的3倍。因此可以說這種情況下φ48×3.5鋼管的安全度比φ25鋼筋大。我們在一個外徑僅2.4m高30m的水塔筒身滑模中,只采用了一些正常的滑升措施(如混凝土澆筑方向應正反交替等)整個滑升過程未產生筒身扭轉,水平偏移也僅幾毫米。省卻了糾偏的麻煩。這在φ25鋼筋支承桿滑模中是不可能做到的,這也從一個側面證實φ48×3.5鋼管支承桿的剛度大、安全度高。也說明了φ48×3.5鋼管支承桿究竟應如何計算還需進一步研究,目前這種計算方法是偏于保守的算法。
3、關于支承桿與千斤頂的配套問題。一般液壓滑模用千斤頂作為一個機械產品,在其出場時需進行耐壓試驗,其試驗壓力應是額定油壓(即相當于額定荷載之油壓)1.5倍。當千斤頂與支承桿共同工作時其安全系數應該相同。現在都取k=2。φ48×3.5鋼管屈服時承載能力為117kN,也就是穩定驗算時折減系數φ=1就是其最大的承載能力。由此推出相應的千斤頂的試驗荷載則為120kN。其額定荷載為80kN。這樣兩者的安全系數就相等了。如果千斤頂的額定荷載再增大,則其配套的鋼管就要加大。如仍用φ48的直徑就需加大的鋼管的厚度。否則就不經濟了。
以上資料收集于網絡,如果版權之爭,請留言。
(本平臺"常州精密鋼管博客網"的部分圖文來自網絡轉載,轉載目的在于傳遞更多技術信息。我們尊重原創,版權歸原作者所有,若未能找到作者和出處望請諒解,敬請聯系主編微信號:steel_tube,進行刪除或付稿費,多謝!)