● 斷裂韌性是指含裂紋材料抵抗快速失穩斷裂的能力。
實際工程結構中,比如大型轉動件、高壓容器、船舶、橋梁等,有時在工作應力遠低于屈服應力下發生了低應力的脆斷。大量失效案例分析后表明,這種破壞是與零部件本身存在裂紋及其裂紋的疲勞擴展有密切關系,典型的斷口形貌如圖2-18、圖2-19 所示。
一般而言,零部件及材料本身難免存在因冶金、加工、焊接等過程引入的加工缺陷,如微裂紋。在外加應力尤其是疲勞載荷作用下,有的微裂紋在使用中發展成宏觀裂紋。一旦裂紋尺寸達到材料固有的臨界尺寸時,便會失穩擴展,發生低應力的脆斷。


圖2-23脆性斷裂斷口形貌
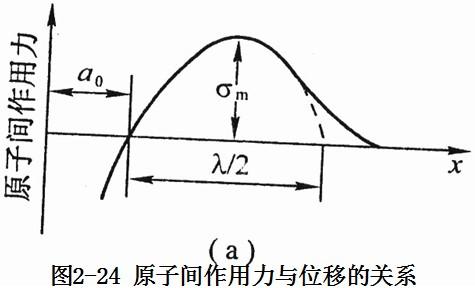
事實上,晶體材料的理論斷裂強度可用圖2-24所示的原子鍵合力進行估算。
● 材料的拉斷是晶體材料在拉應力作用下沿與拉應力垂直的原子面被拉開的過程。
在這一斷裂過程中,外力作的功消耗在斷口上,即斷口的表面能。
設想完整的晶體材料被解理面分開成兩半晶體,其解理面的晶面間距為a0, 沿拉力方向發生相對位移x, 當位移很大時,位移和作用力的關系并不是線性關系。而原子間的相互作用力最初是隨x的增大而增大,但達到一峰值σm后就逐漸下降,見圖2-24。
為了近似地求出圖2-24下的面積,用正弦函數描述應力的變化趨勢,其關系式為:
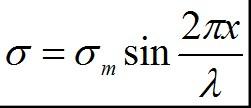
式中λ為正弦曲線的波長,x為原子間距, σm是原子斷開時所需的最大應力,即晶體的理論斷裂應力。
當斷裂發生時,單位面積上作的功可近似表示為:
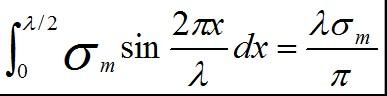
● 晶體拉斷后產生了兩個新表面
令單位面積的表面能用 γs表示。在拉斷過程中,應力所作的功(2-12)應等于表面能 2γs,則有:
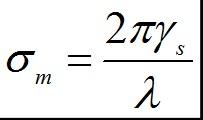
再設曲線開始部分近似為直線,服從虎克定律,即有:
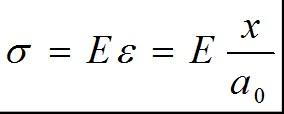
式中a0為平衡狀態時的原子間距。
比較(2-11)、(2-14),得:
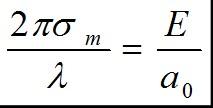
結合關系式(2-13)和(2-15),求得:
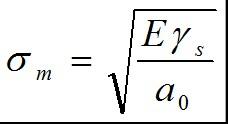
把物性常數E、γs 、 a0分別代入(2-16)中, 就可求得材料的理論斷裂強度(斷裂應力)。

常規碳鋼的抗拉強度約480MPa,因而金屬材料的實際斷裂應力一般是理論斷裂應力σm的1/10~1/100,陶瓷材料和高分子材料則更低。為什么二者會相差如此之多?
其實,早在1921年,英國Griffith就發現材料的實際強度遠低于理論強度,其原因在于材料內部存在固有的缺陷。于是,他研究了陶瓷、玻璃的脆性斷裂的機理問題。
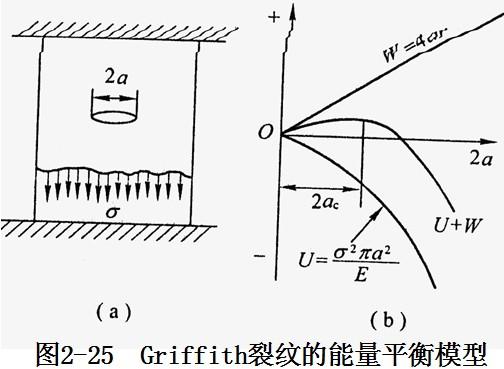
他假定有一塊單位厚度的薄板,兩端在遠處被固定并作用均勻拉伸應力σ。如果板內有一個長為2a的穿透裂紋,裂紋擴展的驅動力來自系統內部存儲的彈性能釋放, 如圖2-25所示。若裂紋發生擴展,則裂紋面積會增加,增加單位面積所需的能量叫表面能 γs。


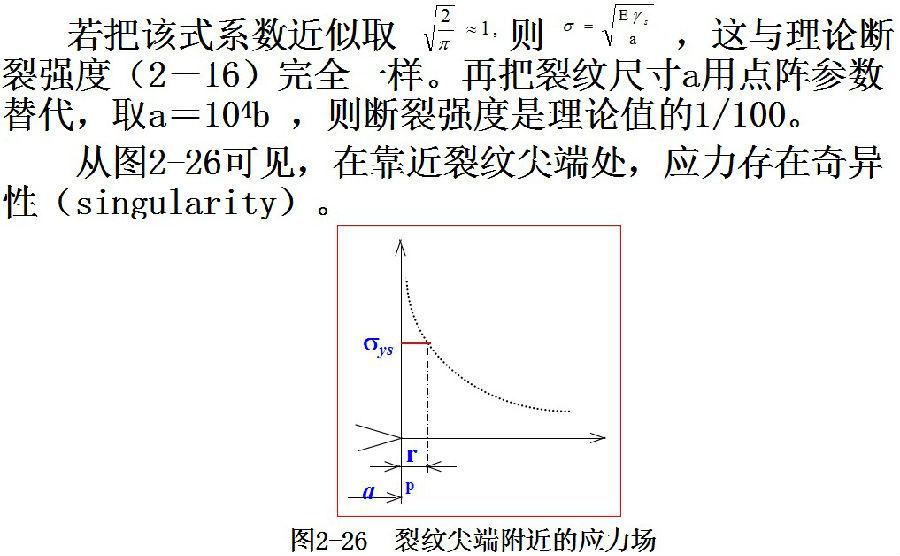
1957年,美國Irwin在Griffith理論基礎上,推導出裂紋尖端附近(圖2-27)的應力場:
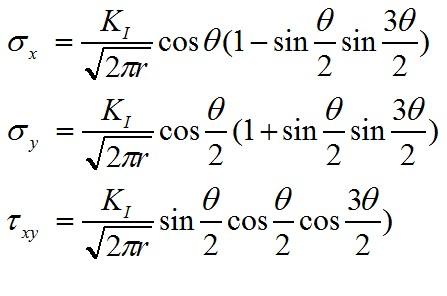
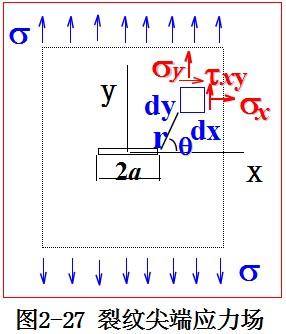
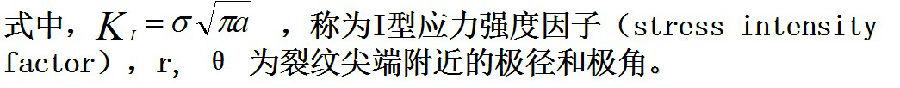

KI與a、σ 之間存在以下的關系式:
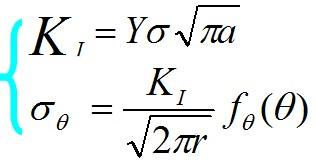
其中, KI的量綱是N/m3/2 ;Y是幾何形狀系數,與試樣尺寸有關,σθ 、 f(θ)分別是裂紋尖端附近的環向應力和角分布函數。
(2-21)、(2-23)式便是現代線性斷裂力學的理論基礎。
由 (2-22)可見,隨外加應力σ的增加,KI也隨之增大,當大到某一臨界值時,裂紋尖端處的應力就達到足以使材料開裂,導致裂紋的失穩擴展:
即 KI = KIC (2-24)
其中, KIC為材料的斷裂韌性值,量綱為N/m3/2。
KIC 值是材料斷裂的性能常數,可以通過斷裂試驗測得。
● KI與KIC和應力σ與σb的關系相似性
對于無裂紋材料,當 σ=σb時,材料因塑性大變形而發生塑性斷裂。 σ 是一個外加的、變化的應力, σb是材料的強度值,是一個固有的不變量,即物性常數。
同樣地,對于含裂紋材料, 當 KI=KIC,材料發生脆性斷裂, KI是一個隨外力而變化的應力強度因子值,KIC是材料的斷裂韌性值,是一個固有的不變量。
因此, σb 是材料的強度性能指標,而KIC是材料抵抗I型載荷裂紋失穩擴展的斷裂性能指標,尤其是脆性材料斷裂時的強度判據。
根據應力作用方式的不同(圖2-28),材料的應力強度因子值共分張開型KI、滑開型KII、撕開型KIII 三種類型。
通過三種類型的加載方式,可分別測得材料的斷裂韌性:KIC、KIIC、KIIIC, 這些值是材料防脆性斷裂的設計判據。
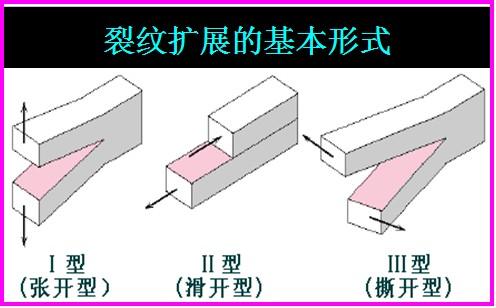
圖2-28 不同類型的應力強度因子
● 斷裂力學進展
從材料變形看,裂紋尖端受外加應力作用后會有一定量的塑性變形,只是塑性變形程度大小不同而已。
因此,當今斷裂力學已從原先的脆性斷裂力學發展到彈塑性斷裂力學。后又發展了考慮材料塑性變形的斷裂韌性參數值,如J積分、裂紋張開位移COD、應變能擴展速率G等。
這些彈塑性斷裂力學參數可以更好地反映材料斷裂前發生一定量的塑性變形的斷裂行為和損傷機理,為結構的可靠性設計提供了重要的理論依據。
不少成果已編入材料抗斷裂設計的評定規范中,如 API法、 R6法、EPRI法、PD-6493法、ASME及我國的CVDA法等 。

| |

