材料發(fā)生形變時(shí),內(nèi)部產(chǎn)生了大小相等但方向相反的反作用力,抵抗外力把分布內(nèi)力在一點(diǎn)的集度稱為應(yīng)力 (Stress),應(yīng)力與微面積的乘積即微內(nèi)力或物體由于外因(受力、濕度變化等)而變形時(shí),在物體內(nèi)各部分之間產(chǎn)生相互作用的內(nèi)力,以抵抗這種外因的作用,并力圖使物體從變形后的位置回復(fù)到變形前的位置。我們分析后查看應(yīng)力,目的就是在于確定該結(jié)構(gòu)的承載能力是否足夠。那么承載能力是如何定義的呢?比如混凝土、鋼材,應(yīng)該就是用萬(wàn)能壓力機(jī)進(jìn)行的單軸破壞試驗(yàn)吧。也就是說(shuō),我們?cè)贏NSYS計(jì)算中得到的應(yīng)力,總是要和單軸破壞試驗(yàn)得到的結(jié)果進(jìn)行比對(duì)的。所以,當(dāng)有限元模型本身是一維或二維結(jié)構(gòu)時(shí),通過(guò)查看某一個(gè)方向,如plnsol,s,x 等,是有意義的。但三維實(shí)體結(jié)構(gòu)中,應(yīng)力分布要復(fù)雜得多,不能僅用單一方向上的應(yīng)力來(lái)代表結(jié)構(gòu)此處的確切應(yīng)力值——就出現(xiàn)了強(qiáng)度理論學(xué)說(shuō)。
材料力學(xué)中的四種強(qiáng)度理論 該理論認(rèn)為,材料破壞的主要因素是最大拉應(yīng)力,無(wú)論何種狀態(tài),只要最大拉應(yīng)力達(dá)到材料的單向拉伸斷裂時(shí)的最大拉應(yīng)力,則材料斷裂。其中,某點(diǎn)的最大拉應(yīng)力數(shù)值,就是其第一主應(yīng)力數(shù)值。 該理論認(rèn)為,引起材料破壞的主要因素,是最大拉應(yīng)變。無(wú)論何種狀態(tài),只要最大拉應(yīng)變達(dá)到材料拉伸斷裂時(shí)的最大應(yīng)變值,則材料斷裂。此時(shí),形式上將主應(yīng)力的某一綜合值與材料單向拉伸軸向拉壓許用應(yīng)力比較,這個(gè)綜合值就是等效應(yīng)力——equivalent stress。 該理論認(rèn)為,引起材料屈服的主要因素是最大切應(yīng)力,不論何種狀態(tài),只要最大切應(yīng)力達(dá)到材料單向拉伸屈服時(shí)的最大切應(yīng)力,則認(rèn)為材料屈服。 該理論認(rèn)為,彈性體在外力作用下產(chǎn)生變形,荷載做功、彈性體變形儲(chǔ)能,稱之為應(yīng)變能(分為畸變能和體積的改變能)。引起材料屈服的主要因素是畸變能密度,無(wú)論何種狀態(tài),只要畸變能密度達(dá)到材料單向拉伸屈服時(shí)的畸變能密度,材料就屈服。
對(duì)于各向同性材料的屈服準(zhǔn)則 當(dāng)材料中的最大剪應(yīng)力達(dá)到某一臨界值時(shí),材料發(fā)生屈服。該臨界值取決于材料在變形條件下的性質(zhì),而與應(yīng)力狀態(tài)無(wú)關(guān)。因此,屈雷斯加屈服準(zhǔn)則又被稱為最大剪應(yīng)力準(zhǔn)則,表達(dá)式為 材料質(zhì)點(diǎn)產(chǎn)生屈服的條件,是當(dāng)其單位體積的彈性形狀變化能達(dá)到某一臨界值,該臨界值只取決于材料在變形條件下的性質(zhì),而與應(yīng)力狀態(tài)無(wú)關(guān)。因此,米塞斯屈服準(zhǔn)則又稱為彈性形狀變化能準(zhǔn)則,其表達(dá)式為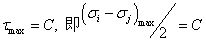
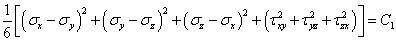
若用主應(yīng)力表示為
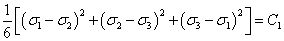
ANSYS后處理中應(yīng)力查看總結(jié)
平面結(jié)構(gòu),查看某方向應(yīng)力;
實(shí)體脆性結(jié)構(gòu),如混凝土、巖石、鑄鐵等,根據(jù)第一、第二強(qiáng)度理論,查看項(xiàng)目為第一主應(yīng)力或等效應(yīng)力;
塑形較強(qiáng)的實(shí)體結(jié)構(gòu),根據(jù)第三、第四強(qiáng)度理論,查看項(xiàng)目為應(yīng)力強(qiáng)度 (stress intensity) 或Von Misses應(yīng)力;
總的來(lái)說(shuō),宗旨就是把各項(xiàng)分布的應(yīng)力,換算成單向應(yīng)力,與規(guī)范規(guī)定的容許應(yīng)力進(jìn)行比較;
von Mises stresses在力學(xué)中是叫馮.米塞斯應(yīng)力,在有限元分析中經(jīng)常會(huì)出現(xiàn)von Mises seqv就是馮.米塞斯等效應(yīng)力,這個(gè)要在《彈塑性力學(xué)》查看;
von mises stresses叫做等效應(yīng)力,與表面壓力完全不是一個(gè)概念,同時(shí)等效應(yīng)力是根據(jù)具體情況而定的,如果第一主應(yīng)力影響最大,那么它幾乎就等于第一主應(yīng)力,如果生物材料中剪切應(yīng)力最大,它就與剪切應(yīng)力近似相等;
von Mises stress是計(jì)算物體的畸變能。
應(yīng)力可以分成兩種,一個(gè)是改變大小的應(yīng)力(Hydrostatic:東西置入靜水壓的情況),一個(gè)是改變形狀的應(yīng)力。而von Mises stress是屬于第二種情形,有很多人會(huì)用Von Mises stress來(lái)分析結(jié)果,但前提是延性 (ductile) 材料(例如:韌帶)才適合用Von Mises stress來(lái)分析。
mises stress實(shí)際上就是應(yīng)力偏量的第二不變量 (J2),應(yīng)力偏量的表達(dá)形式更簡(jiǎn)潔。但這都不是重點(diǎn),重點(diǎn)是它出現(xiàn)最常用的屈服準(zhǔn)則中,原因是它形式簡(jiǎn)單,最容易放到計(jì)算中去,跟簡(jiǎn)單拉伸應(yīng)力應(yīng)變關(guān)系有直接的對(duì)照(在偏量表達(dá)式中,mises stress 和effective plastic strain 那些奇怪的2/3、3/2就是為了和簡(jiǎn)單拉伸關(guān)系對(duì)應(yīng))。在最常用的associate plasticity law中,屈服面的函數(shù)也就是勢(shì)函數(shù),所以mises stress在流動(dòng)準(zhǔn)則中也很重要。因此在很多以微裂紋,孔洞為基礎(chǔ)的損傷力學(xué)中,它和靜水壓一起可以作為損傷的參數(shù)。
后處理節(jié)點(diǎn)應(yīng)力中x、y、z方向應(yīng)力和第一、二、三主應(yīng)力就不介紹了,stress intensity(應(yīng)力強(qiáng)度)是由第三強(qiáng)度理論得到的當(dāng)量應(yīng)力,其值為第一主應(yīng)力減去第三主應(yīng)力。Von Mises是一種屈服準(zhǔn)則,屈服準(zhǔn)則的值我們通常叫等效應(yīng)力。Ansys后處理中"Von Mises Stress"我們習(xí)慣稱Mises等效應(yīng)力,它遵循材料力學(xué)第四強(qiáng)度理論(形狀改變比能理論)。
第三強(qiáng)度理論認(rèn)為最大剪應(yīng)力是引起流動(dòng)破壞的主要原因,如低碳鋼拉伸時(shí)在與軸線成45度的截面上發(fā)生最大剪應(yīng)力,材料沿著這個(gè)平面發(fā)生滑移,出現(xiàn)滑移線。這一理論比較好的解釋了塑性材料出現(xiàn)塑性變形的現(xiàn)象,形式簡(jiǎn)單,但結(jié)果偏于安全。第四強(qiáng)度理論認(rèn)為,形狀改變比能是引起材料流動(dòng)破壞的主要原因,結(jié)果更符合實(shí)際。
一般脆性材料,鑄鐵、石料、混凝土,多用第一強(qiáng)度理論。考察絕對(duì)值最大的主應(yīng)力。一般材料在外力作用下產(chǎn)生塑性變形,以流動(dòng)形式破壞時(shí),應(yīng)該采用第三或第四強(qiáng)度理論。壓力容器上用第三強(qiáng)度理論(安全第一),其它多用第四強(qiáng)度理論。

| |
|
? 請(qǐng)關(guān)注 微信公眾號(hào): steeltuber. 轉(zhuǎn)載請(qǐng)保留鏈接: http://m.youwin2019.com/Steel-Knowledge/1611738068.html
|

