淬火過程中的傳熱特性
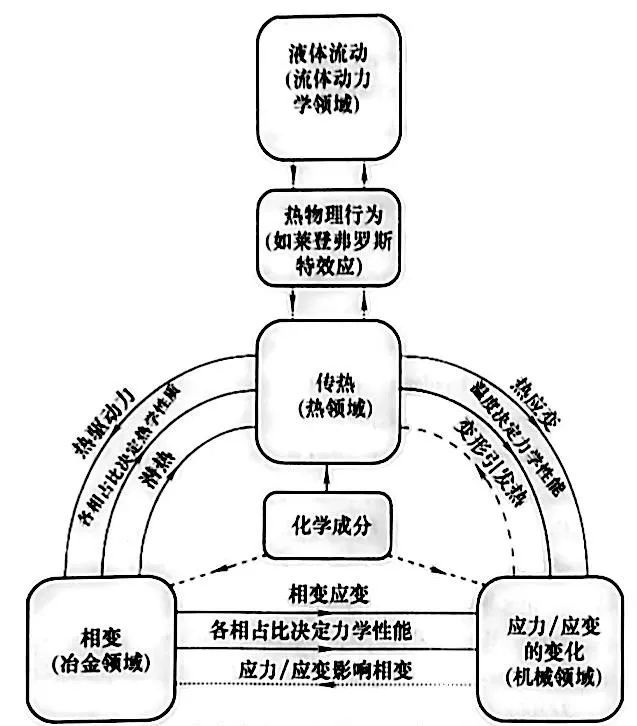
有三個值得研究的方面:
1) 傳熱(隨時間變化,歸因于零件/淬火冷卻介質界面的熱交換)。
2) 相變(隨時間變化,發生各種相變)。
3) 應力應變(隨時間變化,零件內部原子遷移)
因為淬火冷卻介質是液體或氣體,所以淬火冷卻介質的流體動力學對于定義工藝過程中的吸熱很重要。圖1 中給出了造成不同領域相互影響的原因。例如,冶金領域的變化(每種顯微組織容積率的變化)會帶來兩個改變熱領域的影響:相變潛熱的釋放速率和熱物性參數值(取決于溫度和相分布)。
每一個方面的初始狀態都要盡可能精確。習慣做法是假定淬火的開始溫度場是均一的,初始的相變狀態可能包括預先形成的滲碳層、原奧氏體晶粒度、碳化物形成元素全部或部分溶解。初始的應力應變狀態是奧氏體化之后的殘余應力場。
給定的淬火操作能得到的力學性能和變形,是以上各方面在淬火過程中所遵循路徑的綜合結果。鋼淬火的目的是在將奧氏體轉變為馬氏體的同時,保證變形盡可能小。設計、控制和優化淬火過程有三種不同的方法:經驗法、實驗室測試和工藝工程。且所需要的專業技術的復雜程度依次增加。同時,產生知識的量也隨著增長。對于一個給定問題,這三種方法中的任何一種(或者任何組合)都可能是合適的。
溫度高于絕對 “0” 度的所有物體都包含一定量的熱能(內能和動能之和), 大小與其溫度直接相關,由于溫度更容易測量,所以系統的熱能狀態通常用溫度來表征。熱電偶是記錄材料加工過程中溫度變化最常用的工具。熱電偶要么放置在零件內部(鉆孔插入), 要么直接與零件表面接觸。第一種情況下,用各種高溫粘結劑將熱電偶固定到零件上。在有些研究中,會采取措施來防護熱電偶護套和零件之間的熱觸點。保持熱電偶與零件表面接觸的方法有兩種:內在的和外在的。內在的是材料組成了熱電偶環路的一部分,外在的是先將兩個熱電偶導線焊接起來,然后將連接點 點焊到零件表面。茨曾(Tszeng) 和薩拉夫(Saraf) 闡明,在表面安裝熱電偶帶來的鰭效應會影響測量的溫度,因此,他們建立了數學模型來校正它。這個模型能被嵌入一個更一般的零件熱有限元模型中。南馬可探頭(圖2 ) 是在探頭表面鉆垂直于表面的孔來放置熱電偶的尖端的。
與溫度一樣,冷卻速度是熱處理中很重要的一個參數。它不能直接測量,作為替代,是通過測量冷卻曲線將其計算出來的(溫度-時間數據)。通常假設冷卻曲線在一個較短的時間間隔內為線性變化。根據這個假設,可得近似導數的兩點公式:
![]()
(1)
式中,
T-溫度;t-時間;ΔT-在一小段時間(Δt)的溫度變化。
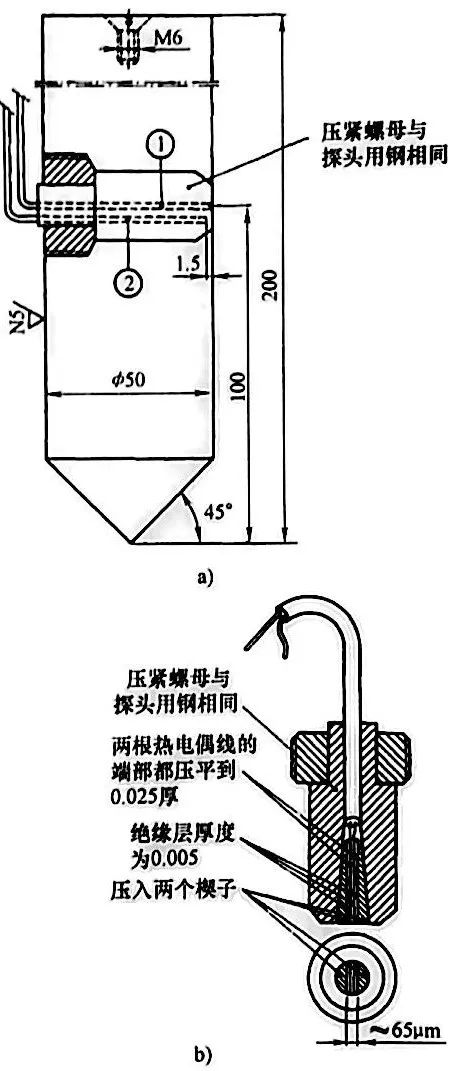
圖2 南馬克探頭
a) 探頭示意圖 b) 熱電偶細節
考慮到研究的是熱響應的量,因此選擇合適的數據采集頻率是很重要的。Totten等人闡明了頻率增加(從1Hz增加到5Hz) 對一個英科鎳600圓柱形探頭 [Φ13 mm (Φ0. 5in)x100mm(4.0in),幾何中心焊接了一個熱電偶)冷卻速度-時間曲線的影響。他們發現,為得到足夠圓滑的曲線需要用最大的頻率。數值導數(如用來計算冷卻速度的) 趨向于形成粗糙的曲線,特別是當采用兩點公式的時候。傳熱過程會讓物體里的溫度分布得到改善。無論物體內部還是物體之間只要存在溫度差(驅動力), 就會發生傳熱。傳熱速度是用熱流量表征的,它與熱流密度和傳熱面積有關,即:
Q=qA⊥ (2 )
改善系統熱平衡的另一種方法是將熱能轉化為另一種形式的能量,反之亦然。例如,當電流流經一個有電阻的材料時,一部分電能就會轉化成熱能并以熱量的形式消散,這就是焦耳效應。另一方面,當吸熱反應發生的時候,熱能會被用來轉化成反應所需要的化學能。
因此,流進系統的熱量,流出系統的熱量,以及轉化成其他形式的或由其他形式轉化來的熱能,結合起來就組成了系統中的熱能凈變,即:
![]()
(3)
注意:式(3 ) 中所有術語的單位都是[熱能/時間], 換言之,表示熱能流,盡管通常都稱其為熱流(并不正確)。
式(3 ) 中的熱能轉化速度(QG) 也稱為熱源(一種形式的能量轉化成熱能)或冷源(熱能轉化成其他形式的能量)。這個術語說明了顯熱和潛熱的區別:前者意味著由于物體傳遞了一個凈熱使溫度發生變化[式(3 ) 中A≠0] , 沒有熱源和冷源;而后者則可能在等溫或非等溫情況下發生,如果流進系統或流出系統的凈熱被相變相關的熱源或冷源抵消掉則是等溫情況[式(3 ) 中A=0] , 如果沒有這樣的平衡則是非等溫情況[式(3 ) 中A≠0] 。
傳熱有兩種基本機理:傳導和輻射。傳導是指系統中的兩個部分通過分子運動進行傳熱,因此它具有短程作用的特征,需要媒介的存在,它不能在真空中發生。傅里葉(Fourier) 提出的現象規律,通過傳導將溫度梯度與熱流密度聯系起來。他發現,熱流密度與溫度梯度成正比關系,比例常數取決于熱量流過的材料。傅里葉定律如下(例如對于x軸方向上的熱流):
![]()
(4)
式中,qk,x為 x 軸方向上傳導的熱流密度;k-材料熱導率;T-溫度。
![]()
式中,qrad-輻射的熱流密度;
σ -常數(5.669×
![]()
);
T-表面溫度(K)。
斯蒂芬-玻耳茲曼公式是由黑體表面公式(黑體輻射定律)推導而來的,黑體表面是一種假定可以吸收所有入射輻射的表面。總之,真實表面放射的輻射能要小于式(5 ) 所預測的值。真實表面輻射熱能qrad,real的計算公式為:
![]()
(6)
在許多教科書里,還有第三種傳熱機制:對流。它的發生是基于表面和流動液體之間的相互作用。當液體在外力作用下流過外表面時,稱為強制對流;而自由對流則是由密度差造成的液體流動。不論是哪種形式,表面與液體之間的傳熱實際上都是通過傳導和輻射發生的。因此,一些作者認為不應把對流劃分為一種傳熱機制。更確切地說,在這種傳熱模式下,傳熱的同時伴隨對流。由于同時解決速率和溫度場(在自由對流時是耦合的,強制對流時是非耦合的)的問題很復雜,通常用牛頓冷卻定律來量化表面和液體之間的傳熱,即:
![]()
(7)
Tf-液體整體溫度,它是熱界面層(這里的溫度梯度較大)以外的液體溫度,被假定為常數。注:許多課本和論文在提到淬火熱處理時、用字母a表示傳熱系數。
可蒸發液體被加熱到飽和溫度(給定氣壓下)以上時發生沸騰,導致從液體到氣體的相變發生;盡管沸騰通常會伴隨著氣泡的形成,但是當表面溫度足夠高時,可能形成蒸汽膜。沸騰的不同模式是按液流的流體動力學和液體相對于飽和點的工作溫度來分類的。如果液體是靜止的,則稱為池內沸騰;如果是由外力造成的液體運動,則稱為強制對流沸騰。注意:氣泡動力學導致工件表面附近為兩種模式的組合。當液體工作溫度保持在飽和點以下時,發生欠熱沸騰。另一方面,當液體保持在略高于飽和點的溫度時,發生飽和沸騰。至于試驗研究中或工廠操作中的熱力學條件,可能是穩態的(用電力控制或用表面溫度控制)或瞬態的。
對沸騰的研究大部分都集中在飽和池內沸騰上。在一項開創性研究中,拔山(Nukiy-ama) 設計了一種電力控制設備,用于描述大氣壓下靜水的沸騰行為。他將一根Φ0.14mm (Φ0.006in)的鎳鉻合金絲在100℃ (212°F) 的靜水中加熱,然后將表面熱流密度(qs ) 作為相應壁面過熱度(ΔTsat, 也就是表面溫度和液體飽和溫度之差)對數的函數繪制成圖。這個圖稱為沸騰曲線。他觀察到,表面熱流密度隨著壁面過熱度的增加而增加,直到達到一個最大值,沸騰曲線有局部極小值,并且在很高的壁面過熱度下將發生熔斷效應。從他的觀察來看,可以在沸騰曲線上定義核沸騰與膜沸騰區域。核沸騰區域涉及形核、長大和氣泡分離,它在沸騰曲線的上限處,由表面熱流密度極大值定義,又稱臨界熱流密度。另一方面,在膜沸騰階段,蒸汽膜覆蓋表面。臨界熱流密度在核反應堆設計中至關重要。
拔山的試驗是在穩態條件下進行的,控制流經鎳鉻合金絲的電功率,也就控制了表面熱流密度。在這種試驗條件下,是不可能觀察到核沸騰與膜沸騰之間的區域的。池內沸騰條件下的完整沸騰曲線如圖 3 所示。由于動力學因素限制了氣泡成核,因此需要少量的過熱度(區域 I ) 來促使氣泡形成。
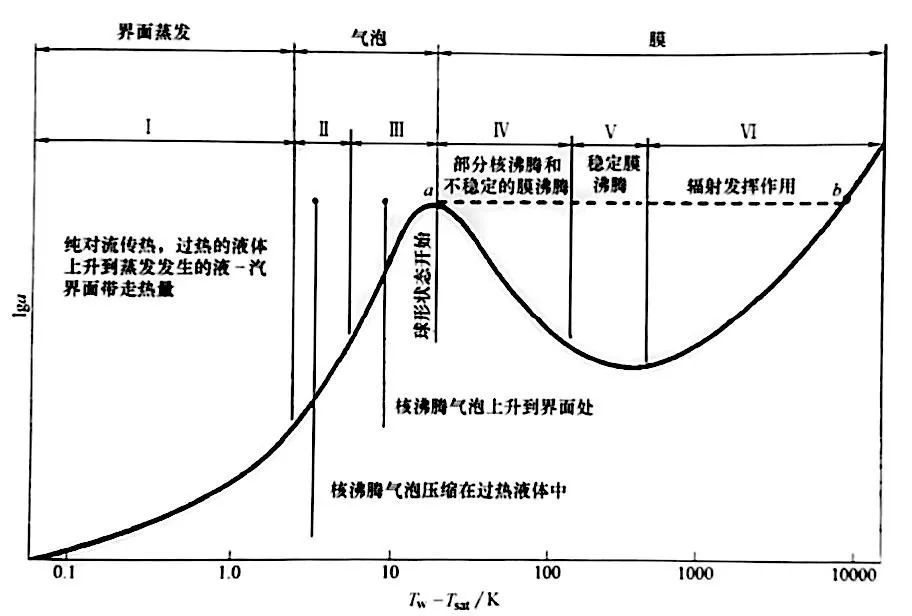
池內沸騰的液流主要受氣泡的運動所驅動、而在強制對流沸騰中,整體運動連同力效應是造成液體流動的主要原因。對給定的欠熱沸騰、當液體流速增加時,吸熱也在增加,如圖4 所示。
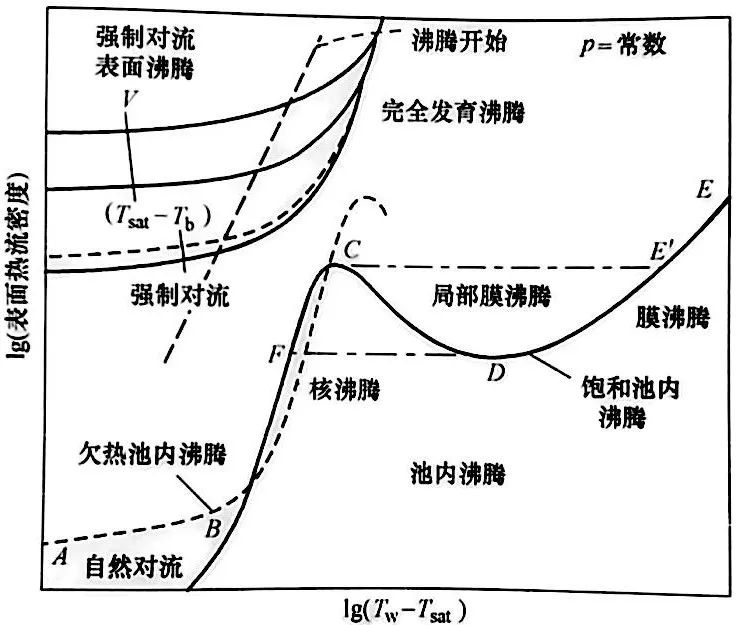
▲圖4 強制對流沸騰與池內沸騰的對比
比池內沸騰所能提供的冷卻速度更高的需求,促進了基于強制對流沸騰的效率更高的冷卻方案的發展。在冶金工業中、噴液冷卻用在鋁合金的壓力淬火上,是因為它加快了沸騰曲線所有區域的傳熱速率。噴液冷卻被用在輸出輥道(軋后冷卻)上,以得到高吸熱速率,使鐵素體晶粒細化,從而使所生產的鋼具有更高的強度。在鋼的連鑄過程中,銅模與冷卻水之間通過強制對流發生熱交換,這加強了向冷卻液體的傳熱,避免了模溫過高,否則會導致澆注缺陷。強烈淬火過程是基于高攪拌淬火冷卻介質的,完全抑制了膜沸騰。其中,射流沖擊是一種非常高效的強制對流工藝。
淬火時,顯微組織的轉變得到最終的顯微組織分布,但是也改變了探頭內的熱平衡狀態。在淬火時,鋼中所有固態轉變都是放熱反應、也就是說發生相變時都會放熱。從奧氏體向其他顯微組分 k 的相變,其單位體積釋放熱(q G,k) 與相交率成正比關系,即:
![]()
(8 )
ΔH -單位質量轉變焓:
fk-顯微組分 k 轉變的比例。
單位體積釋放熱與熱能轉換速度[ 式(3 )中的QG]之間的關系是:
![]()
(9 )
在熱處理條件下、局部熱能轉換速度通常超過局部凈熱流參考 [式(3 ) ]從而導致相變階段溫度-時間曲線上斜率的改變。在加熱的時候,向奧氏體的轉變是吸熱的,導致升溫速度有輕微降低,這是因為熱量被轉變吸收了。
與此相反,在冷卻過程中,轉變是放熱的,也就是說,釋放熱量,導致溫度升高,這被稱為再輝現象。例如,圖5 構造了一條冷卻曲線,是將Φ1.6mm (Φ1/16in) 的K型熱電偶安裝在一個Φ12.7mm×50.4mm ((Φ0.5in×2.0in) 的 AISI 4140鋼制圓柱形探頭中心線上,并將探頭在室溫氧化鋁和空氣的流態床中淬火。
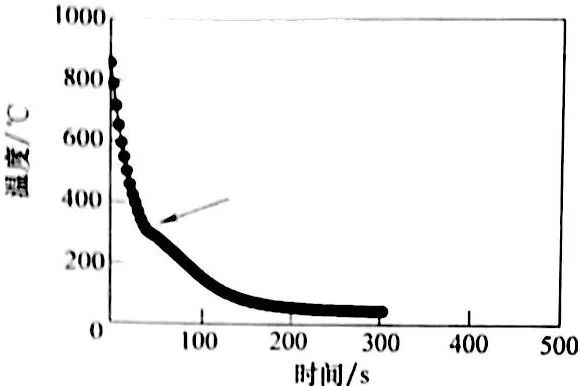
通常用流化數(實際氣流速度與最小流化速度的比值)來表征流化床反應器的流化程度。圖5 里的最終流化數是1.4,表明通過流化床的實際氣流速度是實現流化所需的最小速度的1.4 倍。在淬火初期,溫度單調降低。大約在320℃ (610°F) 左右,斜率有了明顯的改變。這是因為奧氏體向馬氏體轉變釋放的熱量超過了淬火冷卻介質的吸熱能力。如前所述,冷卻曲線上的這種改變稱為再輝現象。到轉變未期,放熱速度被吸熱速度補償掉,度單調降低,直到達到流化床時工作溫度。新在
T-局部當前溫度;
Ms是馬氏體轉變開始溫度;
β=0. 011℃E-1
擴散型轉變(奧氏體轉變為鐵素體,珠光體或貝氏體)發生在高溫區域,考慮等溫轉變情況,可以用約翰遜-梅爾-阿弗拉密-柯洛姆戈洛夫(Johnson- Mehl-Avrami-Kolomgorov) 公式進行數學計算:![]() (11 )
(11 )
b和n是試驗確定的參數。
根據式(9 ) 、式(10 ) 和式(11 ) , 顯而易見,奧氏體在淬火過程中分解的熱能釋放速度取決于相變速度,實際上取決于當前溫度。因此,熱和顯微結構是強耦合的(圖1 ) 。相變動力學與溫度和時間之間的關系已由 TTT 圖給出,如圖6 所示。
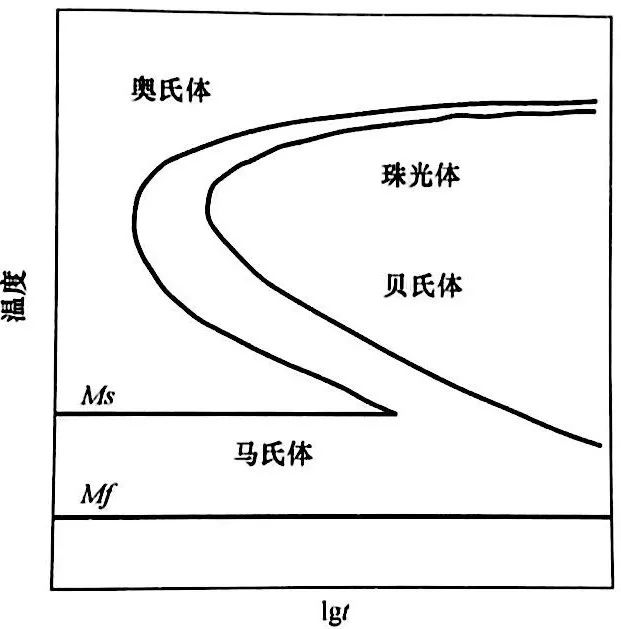
▲圖6 TTT示意圖
標志性的“鼻尖”是高溫轉變中形核和長大競爭的結果。奧氏體向馬氏體轉變開始和結束的溫度稱為馬氏體轉變開始和結束溫度(分別用 Ms 和 Mf 表示)。這類圖是在等溫條件下進行試驗所得到的圖,故也稱為等溫轉變圖。然而淬火是一個非
等溫過程,因此常在連續冷卻轉變圖(CCT )而不是 TTT 圖上疊加一條測得的冷卻曲線來大概地預測最終顯微組織。CCT圖是根據氣體冷卻試驗得到的數據來繪制的。然而,通常淬火時的冷卻條件與氣冷的條件有很大不同,因此,如果用 CCT 圖來做定量預測的話必須謹慎。
三、液體淬火傳熱
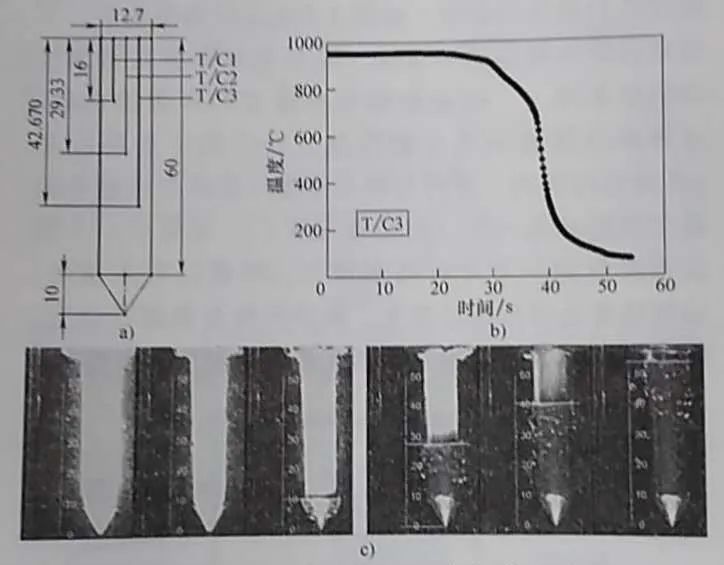
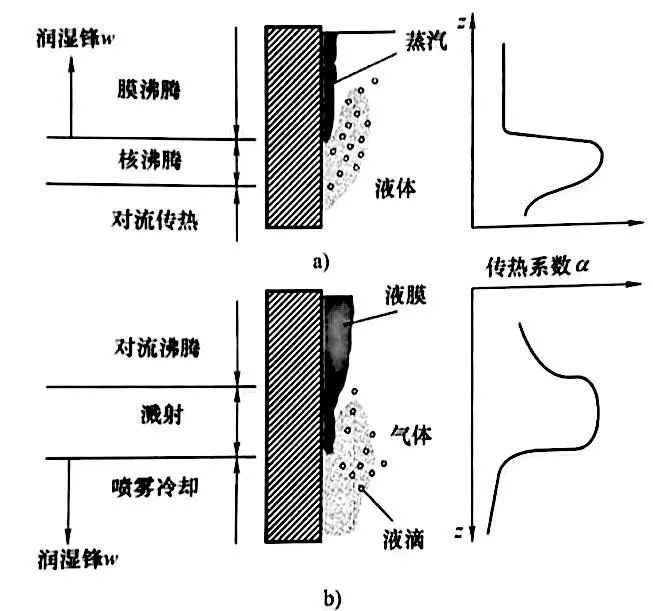
▲圖8 潤濕行為和傳熱系數α
沿金屬探頭表面的變化
a) 浸入冷卻 b) 薄膜冷卻
3.1 再潤濕
根據時間確定了潤濕鋒的位置之后,通過擬合曲線就可以估計潤濕鋒的速度。例如,將末端為圓錐形的圓柱形探頭淬人流速為0.2m/s (0.7ft/s) 的水中(水流與探頭長度方向平行)并進行拍攝,根據從拍攝記錄里提取的照片可以知道潤濕鋒的位置,埃爾南德斯-莫拉萊斯(Hernandez-Morales) 等人擬合了一條回歸線,如圖9 a) 所示。一種衡量線性回歸優度的辦法是使用判定系數(R2 ) 。如果它的值接近1, 則說明因變量與自變量之間有很強的線性關系。圖9 a)中R2的值為0.994, 這說明潤濕鋒位置與時間之間的關系可以假定為線性的,因此,潤濕鋒速度在此例中是不變的。采用同樣的方法,潤濕鋒速度可以計算成浴溫的函數(圖9 b) )。
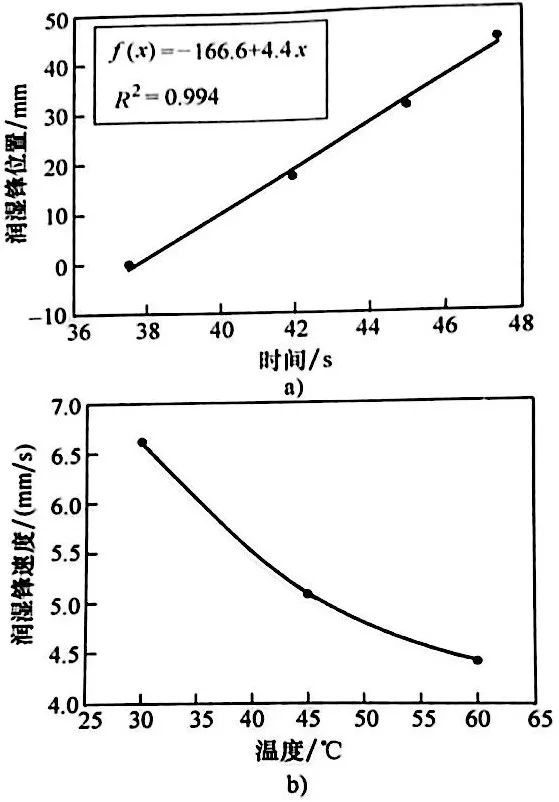
潤濕鋒速度與浴溫之間的關系是非線性的,潤濕鋒速度隨著浴溫的升高而下降,因為這種情況下蒸汽膜更穩定,所以需要更長的局部再潤濕時間。由于相同的原因,局部萊登弗羅斯特溫度隨著水溫的增加而降低(意味著蒸汽膜更穩定)。
除了攝影的辦法,還有替代的辦法來描述潤濕鋒的運動。坤策爾(Kunzel ) 等人注意到,零件表面與一個反電極之間的電導率和蒸汽膜破裂直接相關。他們在一個Φ15mm×45mm (Φ0.6in×1.8in)的圓柱形鉻鎳合金探頭的中心安裝了一個熱電偶,然后測量與探頭同心的圓形背板電極與探頭之間電導率的變化。在對沸水進行試驗的初期,他們測得出的電導率很低,這是因為蒸汽膜不僅是一種好的熱絕緣體,也是一種好的電絕緣體。隨著再潤濕過程的開始和潤濕鋒的移動,擺脫水膜的表面積逐漸增加,測得的電導率也隨之增加。因而,對溫度與電導率的同步測量,允許測量再潤濕開始的時間和溫度,以及在給定時間探頭表面潤濕的比例。根據這
要注意,在他們的試驗中,采用了一個具有光滑表面的探頭(圖10 ) 。
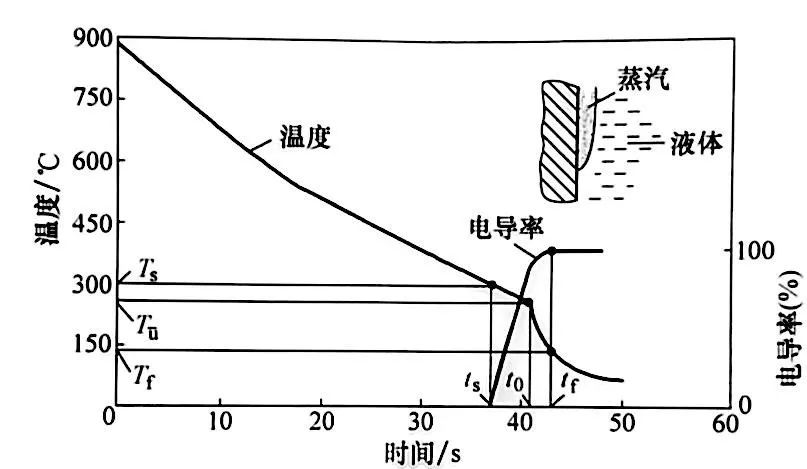
再潤濕開始的時間(t s, 由測量的電導率來確定的)比心部測得的冷卻曲線斜率發生變化的時間(t s) 早。這是探頭表面與其心部之間熱阻導致的直接結果。這個熱阻延遲和抑制了對探頭表面發生的狀況的熱響應。當表面光滑度降低之后(如在表面加工一些螺紋)。試驗時蒸汽膜破裂早得多。但潤濕的表面只有螺紋的頂部部分。因此,測得的電導率增加得很慢,直到沒有氣泡被螺紋捕獲。他們還研究了液槽攪拌和欠溫的影響。發現當任一變量增大時潤濕持續時間都會減少。此外,他們還測量了將 Ck45 鋼從880℃ (1615°F)在50℃ (120°F)水中淬火的最終硬度。他們觀察到沿探頭試樣的硬度分布與潤濕鋒運動一致。
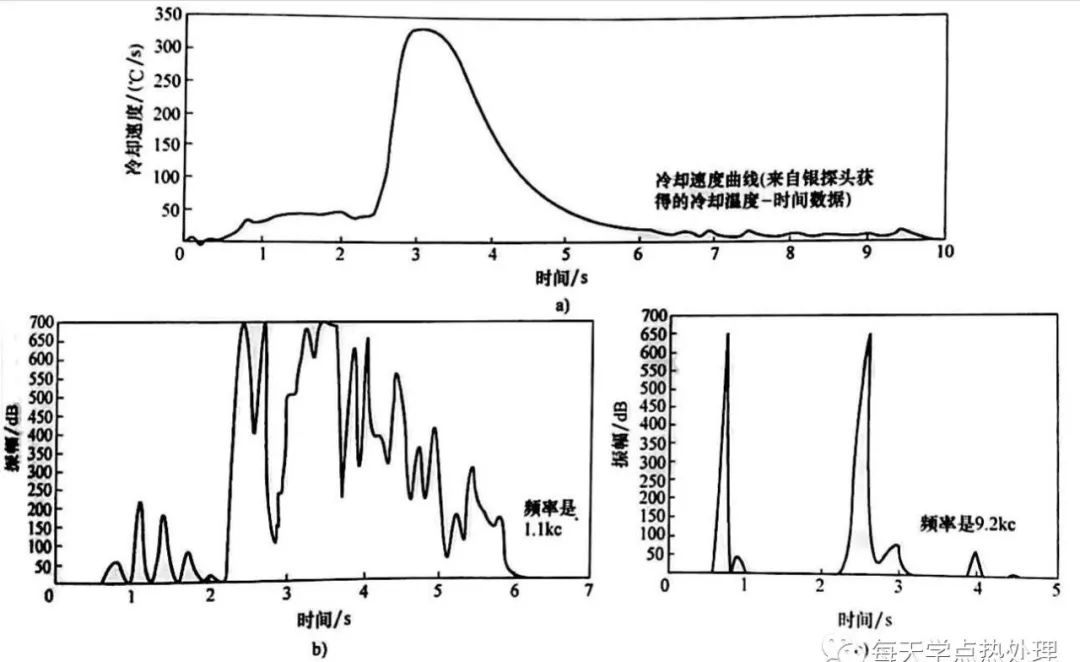
▲圖11 銀球淬火
a)冷卻速度隨時間變化
b)寬波段聲音數據
c)窄波段聲音數據
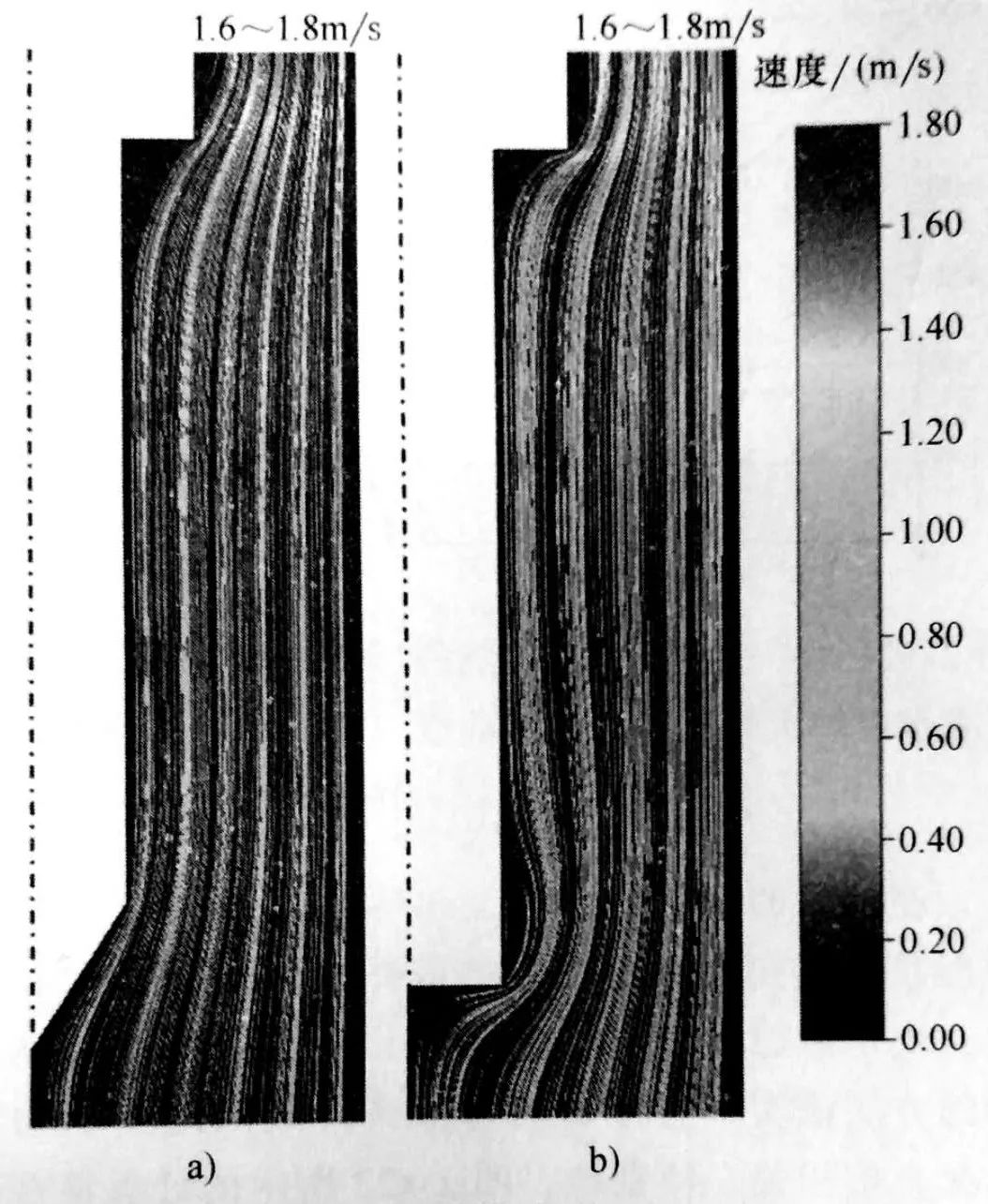
通過攝像記錄(30幀/s ) 和冷卻曲線測量 [將Φ0.5mm (Φ0.02in ) 的鎧裝熱電偶安裝在探頭表面以下大約1mm (0. 04in) 處的方法,弗雷里希斯(Frerichs ) 和呂本(Lubben ) 研究了中空和非中空圓柱體的再潤濕行為。探頭是用303不銹鋼制成的,直徑為50mm (2in) , 長度為100~200mm (4~8in) 。探頭有中空部分和非中空部分。將探頭在N2 保護氣氛下加熱到850℃ (1560°F), 然后淬入 80℃(175°F)的130L靜止高速油中(國際標準速率277 ) , 并確保淬火冷卻介質不會填滿(填充)探頭的中空部分。
一個底部實心上部中空的復合結構探頭的潤濕鋒運動如圖13 所示,兩個部分都沒有螺紋。
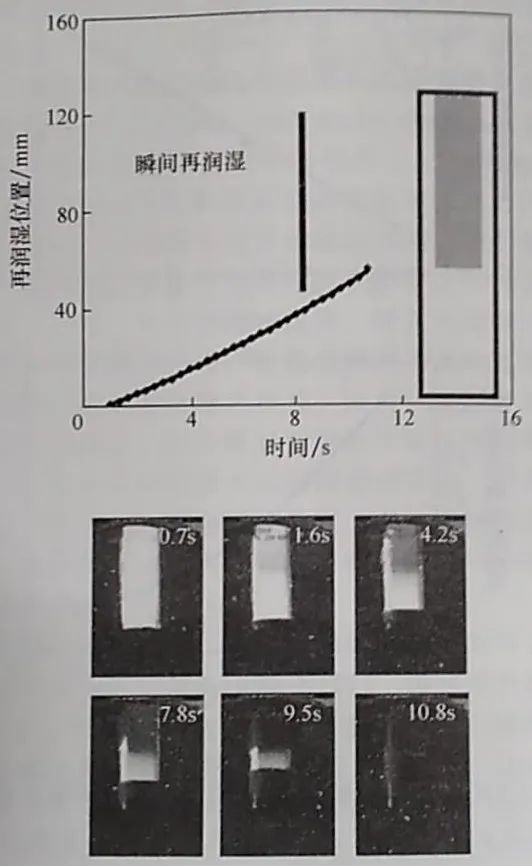
探頭浸入淬火冷卻介質之后,潤濕鋒從底部向頂部(探頭的實心區域)前進。在8s 時,中空部分的再潤濕瞬間發生。在大約10.8s時,兩個潤滑鋒會合于長度方向上的一點,這正是實心和中空部分的交界處。從這個結果看,很明顯,實心部分的量(因為是實心的,所以儲存的熱量多)在再潤濕時起到了重要的作用。固體部分提供的熱量越大,潤濕鋒的速度就越慢,這允許中空部分在前進的潤濕鋒抵達中空部分之前冷到蒸汽膜無法維持的溫度。根據他們所有的試驗,作者總結出潤濕鋒的形成需要形核點,如邊緣或表面奇異點。對于實心部分,作者通過二階多項式,將潤濕鋒的位置擬合成一個時間的函數,這表明實心部分潤濕鋒的速度并穩定。
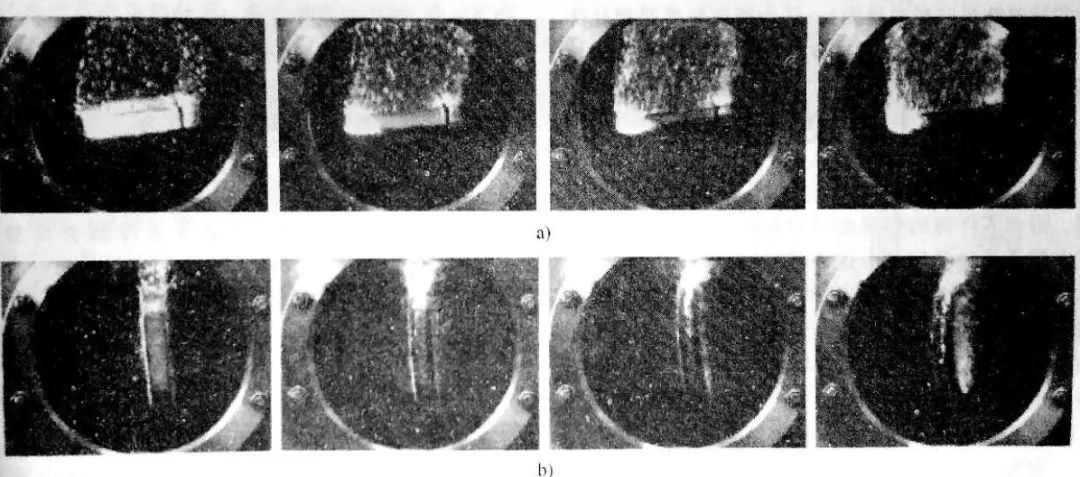
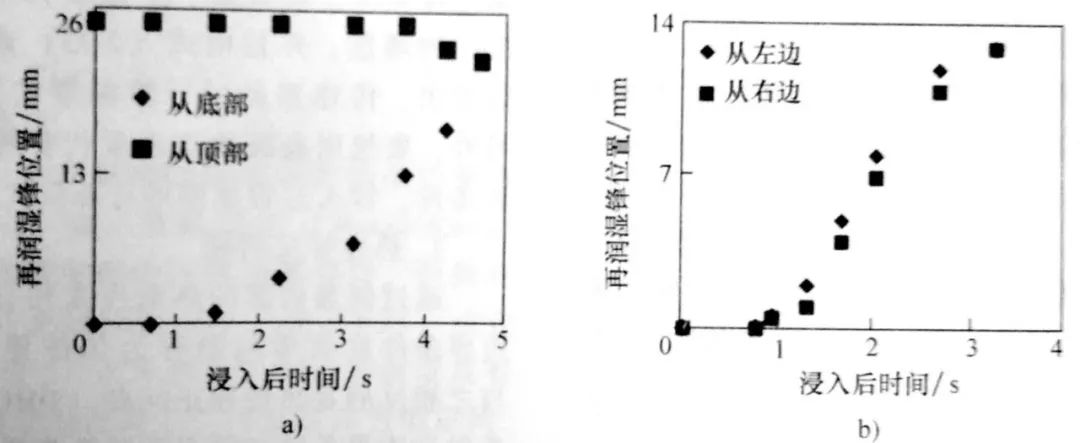
就會觀察到局部最小熱流密度——第二臨界熱流密度(qcr2) 。
3.2 熱溫度場
式中,qG是單位體積的生成熱;
式中,Lc 是與熱傳導有關的特征長度。
習慣上假定初始溫度場是均勻的,因此在區域 Ω 內T 為常數。
式中,![]() 是邊界表面向外的法向。如果式(16 ) 的右側等于零,則稱為齊次邊界條件,簡化了控制方程的解析解。從實用的角度,齊次邊界條件只發生在對稱平面,在這種情況下,諾伊曼(Neumann) 類邊界條件總是齊次的。
是邊界表面向外的法向。如果式(16 ) 的右側等于零,則稱為齊次邊界條件,簡化了控制方程的解析解。從實用的角度,齊次邊界條件只發生在對稱平面,在這種情況下,諾伊曼(Neumann) 類邊界條件總是齊次的。
四、活躍的傳熱邊界條件
在許多研究中,用牛頓冷卻定律來計算傳熱系數的[式(6 ) ] 。用液體欠溫冷卻來計算傳熱系數已成為習慣做法,其計算公式為:![]() (17 )
(17 )
Tf -淬火冷卻介質整體溫度。
但是,科巴斯科提出了異議,他認為應該用表面溫度與淬火冷卻介質的飽和溫度之差來計算,即:![]() (18)
(18)
為了區別二者,科巴斯科將式(17 ) 和式(18 ) 的值分別定義為有效傳熱系數和實際傳熱系數。筆者認為,應該放棄使用傳熱系數,而使用表面熱流密度。后者是一個直接表征零件表面散熱情況的物理量。并且由式(17 ) 或式(18 ) 也可以看出,傳熱系數的計算需要已知表面熱流密度。另外,要想用表面熱流密度代替傳熱系數來作為邊界條件,淬火過程建模的計算機代碼也很容易更改。
通過測量局部的熱響應來估計一個活躍的傳熱邊界條件的數學問題稱為熱傳導反問題(IHCP ) ,與之相反的是熱傳導正問題(DHCP ) (在給定初條件和邊界條件的情況下計算熱領域演繹)。在幾種情況下淬火時需要解決IHCP問題。觀念上,人們對估算熱處理車間實際淬火的活躍傳熱邊界條件感興趣。但是,對于實際幾何形狀復雜、尺寸大的零件,會導致零件表面的傳熱邊界條件的空間分布隨時間而變化,這時可能就需要求解三維(即三個方向的熱流)的 IHCP了。另外,相變的發生,如奧氏體向馬氏體的轉變,使 IHCP 的求解變得更加復雜化。許多研究人員并不去檢測實際零件,而是集中精力研究幾何形狀簡單的相對小的零件或探頭在實驗室級設備里的散熱,此時只有二維熱流甚至是一維熱流的IHCP問題。在許多情況下,材料在淬火時不發生相變。而且在特定條件下,探頭內的溫度梯度甚至可以忽略。
4.2 可以忽略溫度梯度的物體
式中,q (t) 是隨時間變化的表面熱流密度;
式中,h (t ) 是隨時間變化的傳熱系數。注意:由于假設了固體中的溫度梯度可以忽略,通常在式(20 ) 右邊方括號內出現的表面溫度就用T (t) 代替了。式(19) 和式(20 ) 需要定義初始條件,例如:
T (t) =T0,t=0 (21 )
式中,T0 是初始溫度。
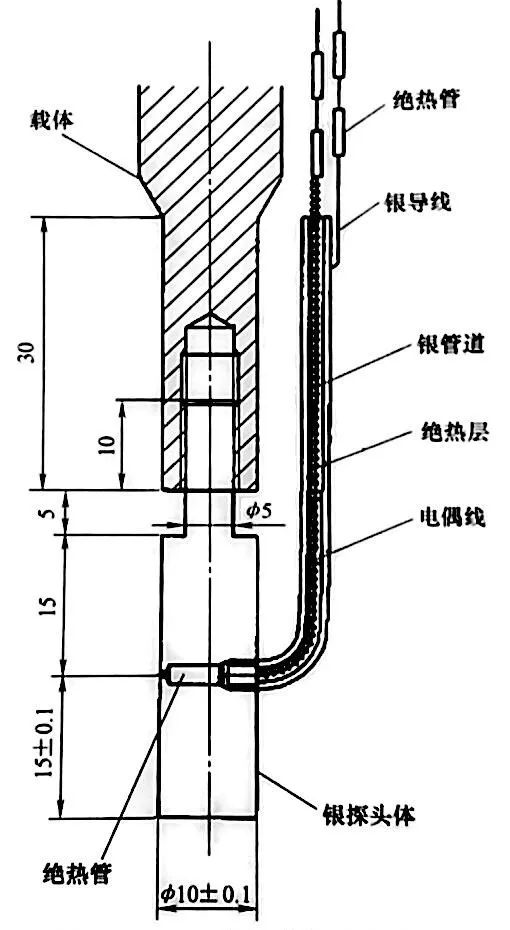
▲圖16 日本工業標準銀探頭
物理性能時,傳熱系數曲線沒有表現出明顯的區別,但是當在計算中使用溫度依賴性熱物理性能時,測得的冷卻曲線與計算得到的冷卻曲線的一致性要好得多(圖17 b)。
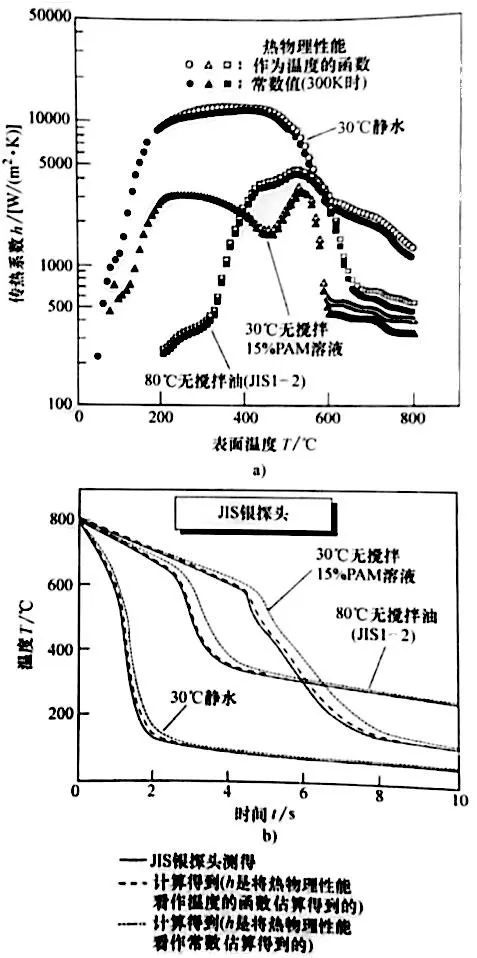
▲圖17 采用不同方法得到的
傳熱系數的冷卻曲線對比
a)作為表面溫度的函數估算的傳
熱系數 b) 測得的與估算的h 條
件下計算得到的冷卻曲線對比
4.3 有溫度梯度的物體
大多數用于描述淬火過程散熱情況的探頭都是圓柱形的,其長徑比應大于 4, 從而確保沒有邊緣效應。基本上,傳熱可以假定為一維的。如果潤濕鋒出現,且有一定的速度,則說明零件在軸向上有明顯的溫度梯度,此時必須考慮二維熱流。但是,為了保持后面的方程式盡量簡單,緩慢移動潤濕鋒的情況將不做分析。按一維熱流假設,探頭的控制方程如下:![]() (22)
(22)
式中,α=k/ (ρCp ) 是熱擴散系數。在中心線上,溫度曲線是均勻的,這意味著溫度的空間導數等于 0 。在固-液界面,液體的吸熱用表面熱流密度或者傳熱系數表征,初始條件認為是均一的初始溫度分布。
式中、Y1 (t )是測得的熱響應。從數學的角度看,IHCP 是一個不適定問題,換句話講,它的解法不具有條件的存在性、唯一性和穩定性。而且 IHCP 的解法對測量誤差很敏感。因為這些特點,大多數具有技術重要性的 IHCP 需要專門的技巧來穩定解法,以得到物理上可信的結果。需要指出的是,所有這些技巧都是將相應的 DHCP 看作 IHCP 算法的一部分。因為活躍傳熱邊界條件通常是高度非線性的,DHCP 不能得到解析解,人們必須求助于數值解法,如有限差分法或有限元法。IHCP 的數值解法可以按順序估算傳熱邊界條件,也就是說,針對每一時間步長估算一個單獨的值,同時估算出全域的傳熱邊界條件的所有值。必須強調的是,IHCP的解只能給出一個估計值,不可能計算出精確的數字。解決IHCP有三種基本方法:函數設定、正則化和迭代正則化。
式中,Y 是測量溫度;T是相應的計算溫度;J 是熱電偶數量;r是將來時間步長數;下標 j 和 i 分別代表熱電偶數量和局部將來時間步長。
對于單獨的熱電偶(J=1),或式(24)可簡化為:![]() (25)
(25)
![]() (26) 或
(26) 或 ![]() (27)
(27)
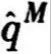 或 h時不必去迭代。同時,一個在
或 h時不必去迭代。同時,一個在 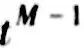 和
和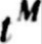 之間的恒定表面熱流密度被用來估算
之間的恒定表面熱流密度被用來估算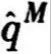 。這個算法的核心是下面的顯式方程,用它來估算只用一個熱電偶的情況下,
。這個算法的核心是下面的顯式方程,用它來估算只用一個熱電偶的情況下,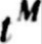 時間的表面熱流密度的值。
時間的表面熱流密度的值。![]() (28)
(28)
其中![]() (29)
(29)
式中,XM+i+1 是靈敏度系數,其公式為:![]() (30)
(30)
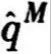 一旦被計算出來就成為下一時間步長的基準點,也就可以估算出暫定值
一旦被計算出來就成為下一時間步長的基準點,也就可以估算出暫定值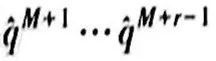 。重復這個步驟,直到達到總時間。為了提高精確度,可以采用小于試驗的計算步長。
。重復這個步驟,直到達到總時間。為了提高精確度,可以采用小于試驗的計算步長。
![]() (31)
(31)
式中,qi 是在時間 ti時估算的表面熱流密度;l 是時間步長總數,即總時間域。不用最小二乘法,通常用伴隨共軛梯度法來使S最小化。
迭代正則法也是一種采用共軛梯度法的全域技術。最小化函數的形式是
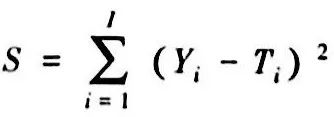 (32)
(32)
貝克等人用試驗數據對比了前面提到的三種方法。試驗裝置包括一個0.86mm (0.034in) 厚的云母加熱器(其中心有一個非常薄的平面電加熱器),加熱器與一個復合材料試樣接觸,試樣另一端是絕緣的。將在云母/試樣界面上測得的試驗熱響應作為輸入,對比了求解IHCP的三種方法,下面的均方根(rms) 表達式可以估算算法中采用的近似值產生的誤差
 (33)
(33)
應該指出的是,一般情況下,表面熱流密度的真實值是未知的。但是,在這種特別的試驗裝置中,通往云母加熱器的電流可以控制,因此進入試樣的熱流密度(qi ) 是已知的,具有很高的精確度。很顯然,這不是普遍情況。雖然三種方法的結果相似,但順序向前選擇算法從概念上講更簡單,也更容易延伸到其他所關注的問題上。
也有其他方法用來解決 IHCP。桑切斯-薩緬托(Sanchez-Sarmiento) 等人假定傳熱系數與時間成線性或多項式關系,用最優化技術估算傳熱系數歷史。科巴斯科等人根據孔德拉特耶夫理論、廣義比渥數及測得的給定溫度下的心部冷卻速度,來估算在植物油里淬火時的有效傳熱系數。
關于熱電偶在探頭或零件中布置的設計,也可以采用兩點法。通過靈敏度系數的概念,可以發現放置熱電偶的最好位置是盡可能接近活躍邊界條件。這與熱電偶和零件表面之間的熱阻較低的推論一致。熱阻較低則減輕了信號的遲滯和阻尼效應,而信號的遲滯和阻尼效應會嚴重影響IHCP算法的效果。探頭在測試區域里總會對該區域造成影響。李(Li) 和韋爾斯(Wells) 發現熱電偶相對于活躍表面的方向對估算的表面熱流密度有顯著影響。熱電偶以與活躍表面成90°角的方向插入會對估算表面熱流密度造成很大的誤差,而與活躍表面平行插入時就不會這樣。他們還推斷,當比渥數很大時,應該將孔(放熱電偶的孔)考慮成相反的熱導模型。在
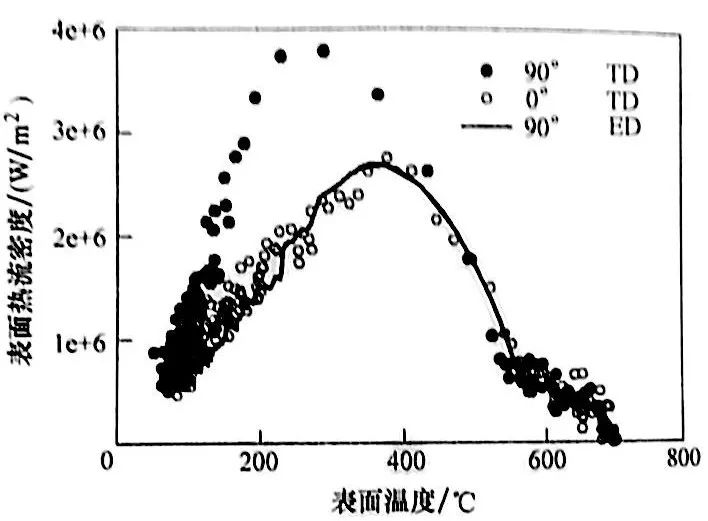
▲圖18 估算的表面熱流密度
作為估算的表面溫度的函數
注:在求解熱電偶平行插入或垂直插入活躍
傳熱表面熱傳導反問題時,分別用實際熱電
偶深度(TD) 和等價熱電偶深度(ED)
4.4 有內發熱的物體
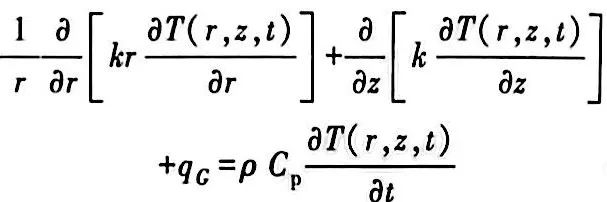 (34)
(34)
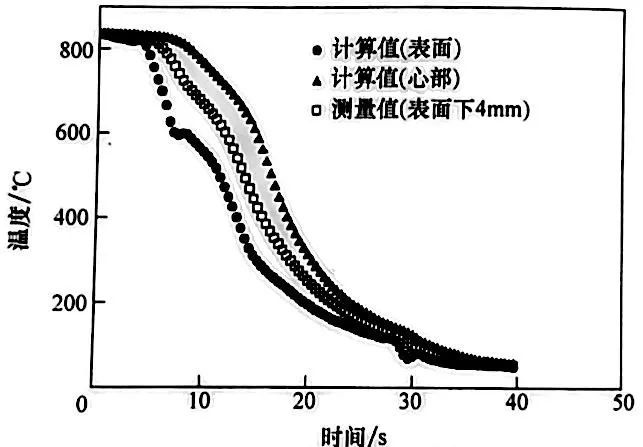
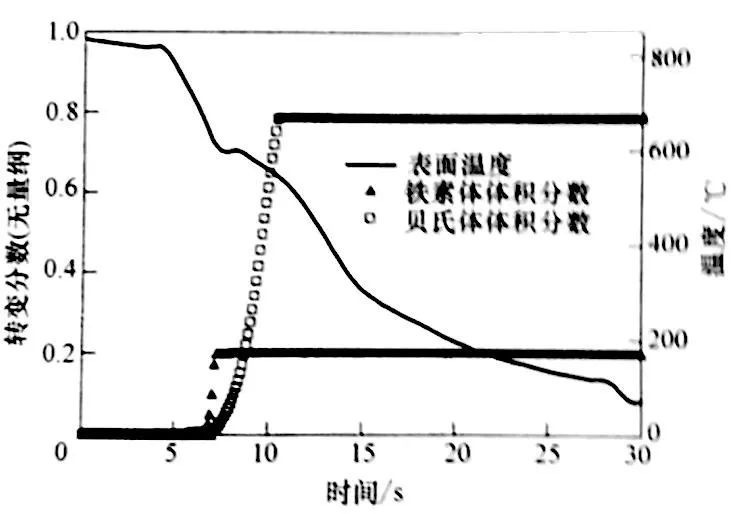
很顯然,在估算的表面冷卻曲線上觀察到的再輝現象歸因于奧氏體向鐵素體以及(尤其是)奧氏體向貝氏體的轉變。研究的主要目標是估算表面熱流密度并解釋其行為。估算的表面熱流密度與估算的表面溫度的關系,以及估算的 AISI 1050鋼探頭淬火過程冷卻曲線如圖21 所示。
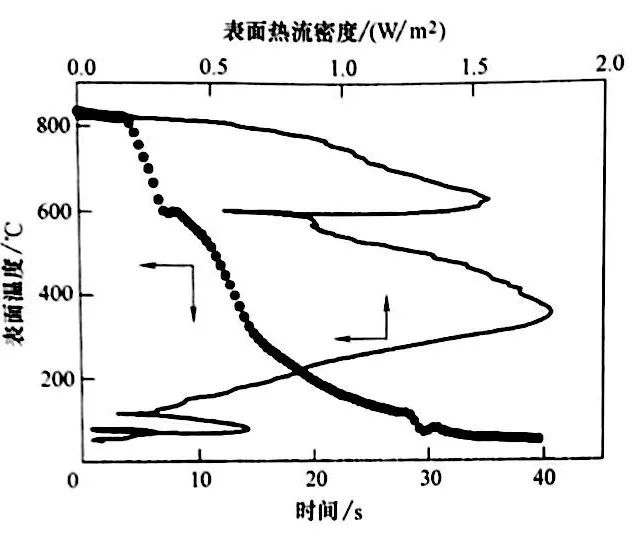
圖中最需要注意的是表面熱流密度曲線出現了兩個峰值。第一個峰值1.6MW/m2, 出現在大約 650℃ (1200F)時。對照探頭表面上體積分數的轉變(圖20 ) , 很明顯,這個局部極大值是由奧氏體向鐵素體轉變開始導致的,而之后的奧氏體向貝氏體的轉變阻礙了估算的表面熱流密度的增加,導致表面熱流密度曲線上的冷卻速度局部降低。轉變一旦結束[大約在550℃ (1020°F) 時], 熱流密度曲線再次上升,直到達到第二個極大值(1.8MW/m2 ) , 這發生在350℃ (660°F)時。因為在這一溫度下表面沒有相變發生,所有第二個極大值只與淬火冷卻介質自身的吸熱特點有關。在100℃ (212°F ) 時可以觀察到一個小得多的局部極大值(0.6MW/m2 ) , 大概對應于水的沸點。從這些結果來看淬火過程的吸熱是傳熱和相變動力學之間錯綜復雜的相互影響的結果。
他們將圓柱形 AISI 4140鋼探頭[Φ12.7mm×50. 8mm (Φ0.5in×2.0in) ] 分別在低于和高于奧氏體化溫度下淬火以得到綜合的熱流密度歷史曲線。通過仔細選擇用于IHCP的冷卻曲線片段,能夠解決不包括相變的問題。
4.5 檢驗
end
相關文章
有一種熱處理方式叫 “逆淬火” !一起了解 “逆淬火” 工藝!!
為什么看《熱處理手冊》后選用油淬火42CrMo軸淬火后還斷裂?
(本平臺"常州精密鋼管博客網"的部分圖文來自網絡轉載,轉載目的在于傳遞更多技術信息。我們尊重原創,版權歸原作者所有,若未能找到作者和出處望請諒解,敬請聯系主編微信號:steel_tube,進行刪除或付稿費,多謝!)

